Building a DGA Classifier: Part 2, Feature Engineering

By “Jay Jacobs (@jayjacobs)"
Thu 02 October 2014 | tags: blog, r, rstats, -- (permalink)

This is part two of a three-part blog series on building a DGA classifier and it is split into the three phases of building a classifier: 1) Data preperation 2) Feature engineering and 3) Model selection.

Back in part 1, we prepared the data and we are starting with a nice clean list of domains labeled as either legitamate (“legit”) or generated by an algorithm (“dga”).

library(dga)
data(sampledga)

In any machine learning approach, you will want to construct a set of “features” that help describe each class or outcome you are attempting to predict. Now the challenge with selecting features is that different models have different assumptions and restrictions on the type of data fed into them. For example, a linear regression model is very picky about correlated features while a random forest model will handle those without much of a hiccup. But that’s something we’ll have to face in when we are selecting a model. For now, we will want to gather up all the features we can think of (and have time for) and then we can sort them out in the final model.

In our case, all we have to go off of is a domain name: a string of letters, numbers and maybe a dash. We have to think of what makes the domains generated by an algorithm that much different from a normal domain. For example, in the Click Security example they calculate the following features for each domain:

Length in characters
Entropy (range of characters)
n-grams (3,4,5) and the “distance” from the n-grams of known legit domains
n-grams (3,4,5) and the “distance” from the n-grams of dictionary words
difference between the two distance calculations

There is an almost endless list of other features you could come up with beyond those:

ratio of numbers to (length/vowels|consonants/non-numbers)
ratio of vowels to (length/numbers/etc)
proportion matching dictionary words
largest dictionary word match
all the combinations of n-grams (mentioned above)
Markov chain of probable combinations of characters

Simplicity is the name of the game

I know it may seem a bit counter-intuitive, but simplicity is the name of the game when doing feature selection. At first thought, you may think you should try every feature (and combinations of features) so you can build the very best model you can, but there are many reasons to not do that. First, no model or algorithm is going to be perfect and the more robust solutions will employ a variety of solutions (not just a single algorithm). So striving for perfection has diminishing returns.

Second, adding too many features may cause you to overfit to your training data. That means you culd build a model that appears to be very accurate in your tests, but stinks with any new data (or new domain generating algorithms in our case). Finally, every feature will take some level of time and effort to generate and process, and these add up quickly. The end result is that you should have just enough features to be helpful, and no more than that. The Click Security example, in my opinion, does an excellent job at this balance with just a handful of features.

Also, there isn’t any exact science to selecting features, so get that notion that science is structured, clean and orderly right out of your head. Feature seelction will, at least at this state, rely heavily on domain expertise. As we get to the model selection, we will be weeding out variables that don’t help, are too slow or contradict the model we are testing.

For now, think of what makes a domain name usable. For example, when people create a domain name the focus on readability so they may include one set of digits together “host55” and rarely would they do “h5os5t”, so perhaps looking at number usage could be good. Or you could assume that randomly selecting from 26 charcters and 10 numbers will create some very strange combinations of characters not typically found in a language. Therefor, in legitimate domains, you expect to see more combinations like “est” and less “0zq”. The task when doing feature selection is to find attributes that indicate the difference. Just as in real life, if you want to classify a car from a motorcycle a good feature may be number of tires on the road, you want to find attributes to measure that seperate legitimate domains from those generated by an algorithm.

N-Grams

I hinted at n-grams in the previous paragraph and they may be a little difficult to grasp if you’ve never thought about it. But they are built on the premise that there are frequent character patterns in natural language. Anyone who’s watched “Wheel of Fortune” knows that consonants like r, s, t, n and l appear a lot more often than m, w, and q and nobody guesses “q” as their first choice letter. One of the features you could include is a simple count of the characters like that (could be called a “1-gram”, “n-gram of 1”, “unigram” or simply “charater frequency” since it’s single charaters). Randomly generated domains would have a much different distribution of characters than those generated based on natural language. That difference should help an algorithm correctly classify between the two.

But you can get fancier than that and look at the frequency of the combination of characters, the “n” in “n-grams” represents a variable length. You could look for the combination of 3-characters, so let’s take a look at how that looks with the stringdist package and the qgrams() function.

library(stringdist)

qgrams("facebook", q=3)

##    fac ook ace ceb ebo boo
## V1   1   1   1   1   1   1

qgrams("sandbandcandy", q=3)

##    san and ndb ndc ndy dba dca ban can
## V1   1   3   1   1   1   1   1   1   1

qgrams("kykwdvibps", q=3)

##    kyk ykw wdv vib kwd dvi ibp bps
## V1   1   1   1   1   1   1   1   1

See how the function pulls out groups of 3 characters that appear contiguously? Also, look at the difference in the collection of trigrams from the first two, they don’t look too weird, but the output from kykwdvibps probably doesn’t match your expectation of character combinations you are used to in the english langauge. That is what we want to capitalize on. All we have to do is teach the algorithm everything about the english language, easy right? Actually, we just have to teach it what should be “expected” as far as character combinations, and we can do that by figuring out what n-grams appear in legitimate domains and then calculate the difference.

# pull domains where class is "legit"
legitgram3 <- qgrams(sampledga$domain[sampledga$class=="legit"], q=3)
# what's at the top?
legitgram3[1, head(order(-legitgram3), 10), drop=F]

##    ing ter ine the lin ion est ent ers and
## V1 161 138 130 113 111 106 103 102 100  93

Notice how we have over 7,000 trigrams here with many of them appearing in a very small proportion, let’s clean those up so the oddities/outliers don’t throw the training. We have 5,000 legit domains, we should be cutting off the infrequent occurances, and we could experiment with what that cutoff should be. But let’s create the n-grams of length 1, 2, 3, 4 and 5, but I will use the function in the dga package called ngram and I’ll recreate the 3-gram above. I’ll also include the ngram of lengths 3, 4 and 5.

legitname <- sampledga$domain[sampledga$class=="legit"]
onegood <- ngram(legitname, 1)
twogood <- ngram(legitname, 2)
threegood <- ngram(legitname, 3)
fourgood <- ngram(legitname, 4)
fivegood <- ngram(legitname, 5)
good345 <- ngram(legitname, c(3,4,5))

Let’s just do a quick smell test here and look at some values with the getngram function in the dga package and how they compare with various n-grams.

good <- c("facebook", "google", "youtube",
           "yahoo", "baidu", "wikipedia")
getngram(threegood, good)

##  facebook    google   youtube     yahoo     baidu wikipedia 
##     7.264     7.550     6.674     2.593     0.699     7.568

bad <- c("hwenbesxjwrwa", "oovftsaempntpx", "uipgqhfrojbnjo", 
           "igpjponmegrxjtr", "eoitadcdyaeqh", "bqadfgvmxmypkr")
getngram(threegood, bad)

##   hwenbesxjwrwa  oovftsaempntpx  uipgqhfrojbnjo igpjponmegrxjtr 
##          2.6812          4.1216          2.9499          2.7482 
##   eoitadcdyaeqh  bqadfgvmxmypkr 
##          3.7638          0.6021

Notice these aren’t perfect and that’s okay, the algorithms you will try out in Part 3 of the series won’t use just one varaible. The strength of the classifier will come from the use all the variables together. So let’s go ahead and construct all the features that we want to use here and prepare for step 3 where you will you will select a model by trying varius classifiers. In a real application, there is a relationship between feature generation and model selection. Algorithms will act differently on different features and after trying a few you may want to go back to feature selection and add or remove some features.

For the sake of simplicity, we will go with these 5 sets of n-grams and the multiple length set used in the the Click Security model.

Prepping the rest of the features

Now that you understand n-grams, you can go ahead and generate the rest of the features and save them off for later. Note that everytime you will want to classify a new domain, you will need to generate the list of features. So the reference n-grams generated above will have to be saved to generate the features that rely on them.

# dga package has "entropy" to calculate entropy
sampledga$entropy=entropy(sampledga$domain)
# get length (number of characters) in domain name
sampledga$length=nchar(sampledga$domain)

# calc distances for each domain
sampledga$onegram <- getngram(onegood, sampledga$domain)
sampledga$twogram <- getngram(twogood, sampledga$domain)
sampledga$threegram <- getngram(threegood, sampledga$domain)
sampledga$fourgram <- getngram(fourgood, sampledga$domain)
sampledga$fivegram <- getngram(fivegood, sampledga$domain)
sampledga$gram345 <- getngram(good345, sampledga$domain)

Note that I am just tossing in every n-gram from 1 to 5 characters and the merging of 3, 4, and 5 n-grams. I doubt that all of these will be helpful and I fully expect that many of these will be dropped in the final model, which I will cover in part 3.

Dictionary matching

There is one last feature I want to add and that will try to answer the question of “How much of the string can be explained by a dictionary?” I’m adding it because I’ve already created several models and found myself getting frustrated seeing a domain like “oxfordlawtrove” being classified as a “dga”, but any human can look at that and see three distinct words. Therfore, I created the function wmatch in the DGA package to return the percentage of characters that are in the dictionary. I also am using the dictionary that was included in Click Security’s code and it seems to be a little loose about what is a valid word. At some point that dictionary could be rebuilt and cleaned up. But, for the sake of time, we can just go with it how it is.

wmatch(c("facebook", "oxfordlawtrove", "uipgqhfrojbnjo"))

## [1] 1.0000 1.0000 0.4286

# calculate it for every word in the sample
sampledga$dict <- wmatch(sampledga$domain)

# and let's look at a few randomly (3 legit, 3 dga)
sampledga[c(sample(5000, 3), sample(5000, 3)+5000), c(6:14)]

##       entropy length onegram twogram threegram fourgram fivegram gram345
## 162     2.725      9   28.52  14.494     6.552   3.6444     1.69  11.887
## 291     1.922      5   16.02   8.868     2.924   0.6021     0.00   3.526
## 473     2.922     10   34.29  20.179     8.397   1.4771     0.00   9.875
## 6519    3.027     13   43.00  19.517     3.085   0.0000     0.00   3.085
## 39999   3.804     24   71.32  21.617     1.833   0.0000     0.00   1.833
## 34989   3.852     28   83.38  22.578     0.699   0.0000     0.00   0.699
##         dict
## 162   0.8889
## 291   1.0000
## 473   1.0000
## 6519  0.4615
## 39999 0.3750
## 34989 0.2143

And because what we want in the features is a seperation in our classes, we can use the fun package GGally to visualize the interaction between some of our varibles (this graphic takes a while to generate).

library(GGally)
library(ggplot2)
gg <- ggpairs(sampledga, 
        columns = c("entropy", "length", "onegram", "threegram", "dict", "class"),
        color="class",
        lower=list(continuous="smooth", params=c(alpha=0.5)),
        diag=list(continuous="bar", combo="bar", params=c(alpha=0.5)),
        upper = list(continuous = "density", combo = "box", params=c(alpha=0.5)),
        axisLabels='show')
print(gg)

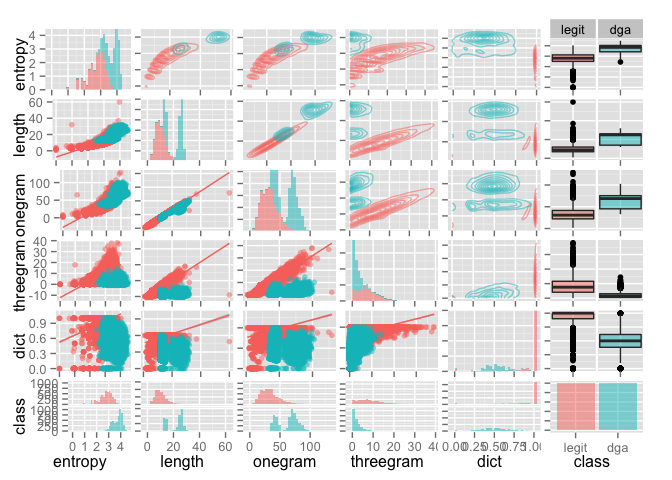
ggally plot

It’s pretty clear in the picture that the last dictionary matching feature I added creates quite a large seperator for the two datasets. Now let’s save off the sample object for use in part 3 of the blog series.

save(sampledga, file="data/sampledga.rda", compress="xz")